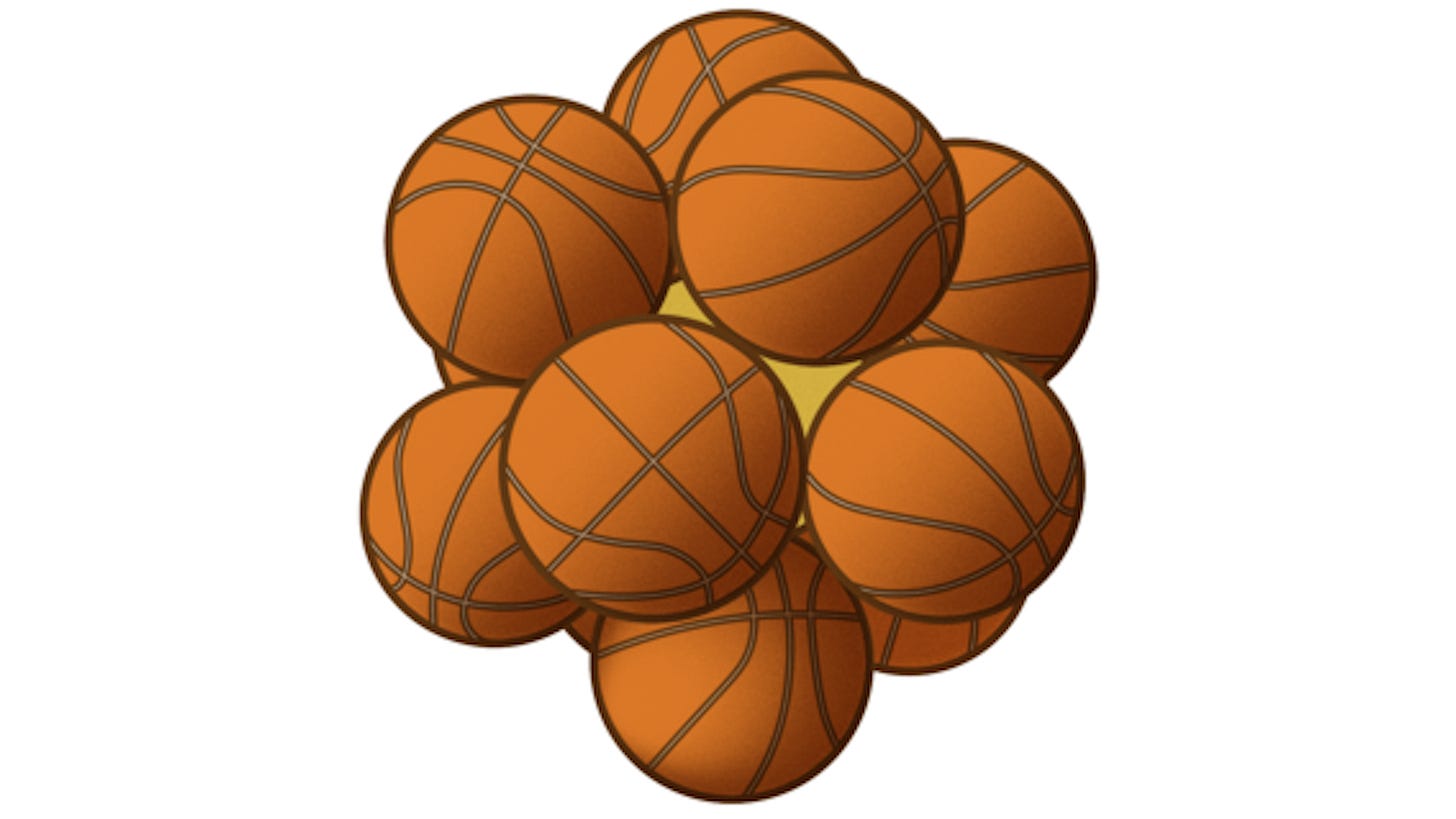
The “kissing problem” isn’t the term for a junior high dance conundrum—it’s actually a reference to a famous mathematical riddle.
The setup is simple: How many circles or spheres can be arranged so that every individual simultaneously touches or “kisses” a single rounded shape in the center?
The answer is relatively simple when dealing with up to three dimensions. The answer for one dimension is 3, two dimensions gets you 6, and a three dimensional situation can support 12 kissing spheres.
In 2003, mathematician Oleg Musin proved that the kissing number for four dimensions is 24. If that concept is hard to wrap your head around, it only gets weirder as the dimensions increase.
Kissing problem experts have been stuck for about two decades. Despite their efforts, no one had established a new lower bound of objects for any dimension below dimension 16.
Read more | POPULAR SCIENCE